GSoC #7: Taking Stock

These past two weeks were, like the one before it, largely about dealing with the implementation in code. In theory, the marginalization routine works from top to bottom, however there are a few outstanding bugs that need to be squashed.

First, the minimize code seems to be incompatible with certain kinds of backprop routines, as pm.sample crashes when it tries to pass gradients through it. This is a PyTensor issue and something Ricardo and Jesse and working on currently. However, using a simplified toy model of the form:

\begin{equation} \theta \sim N(\mu, I) \end{equation}

\begin{equation} x \sim N(\theta, I) \end{equation}

\begin{equation} y \sim N(x, I) \end{equation}

We can obtain the closed-form solution \(x_0(\theta) = \frac{1}{n-1}(\Sigma_i^n y_i - \theta)\) (assuming my math is right) instead of using minimize, which allows us to test the rest of our code against simply sampling over \(x\) directly with pm.sample. Doing this gives good results, with both direct sampling and INLA providing similar means. Note that shifting \(x_0\) by some amount shifts the posteriors also, which suggests that the current implementation (and also the closed-form solution) is valid.

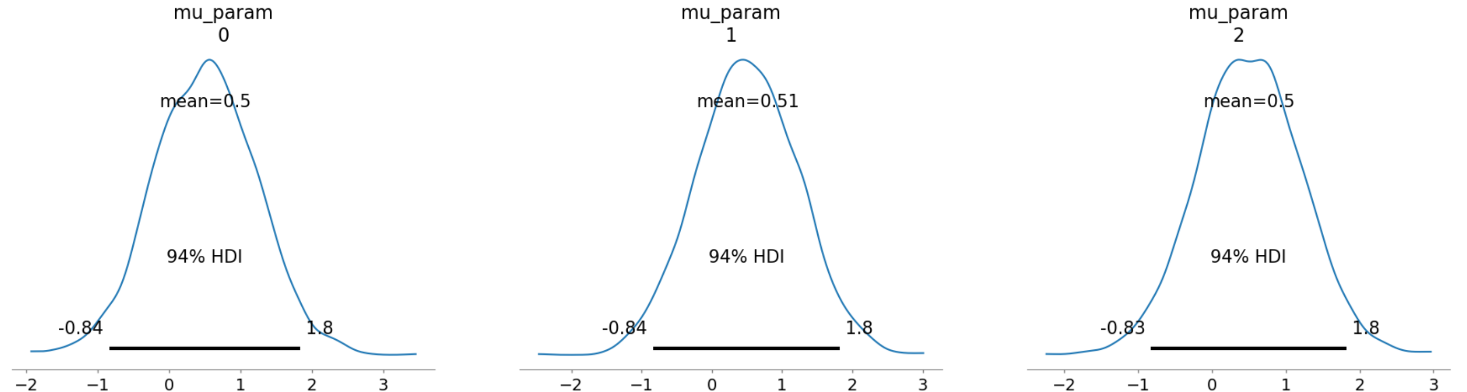
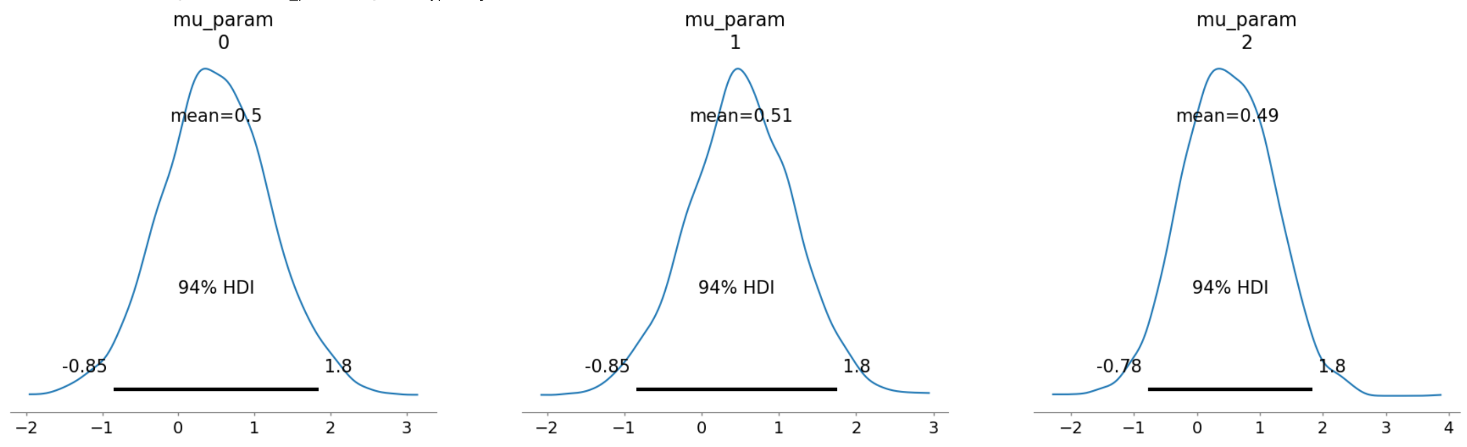Top: Direct sampling. Bottom: INLA.

However, I will still need to ensure that the posteriors integrate up to unity, as the Laplace approximation is only a normalising constant, however given that \(x_0\) is fine, this is unlikely to have any issues. The next step in the INLA roadmap was to implement the adjoint method of differentiating \(x_0(\theta)\), as backpropping through several minimizer iterations is very expensive, but it turns out that Ricardo and Jesse already implemented that into minimize natively so hopefully this is already done! However, previous testing suggested that calling pm.sample with minimize was very expensive, so we may need some optimisations here.

Aside from ensuring the Laplace approximation is valid, the algorithm is just about ready, only needing to get the latent posterior \(p(x \mid y)\), which hopefully shouldn’t be too difficult (simply a matter of plugging \(p(\theta \mid y)\) back in). I just need to tidy things up and make a neat API out of it.